Meijer's G-function is a universal function that, with the appropriate choice, can reproduce many commonly used smooth functions, including trigonometric, exponential, logarithmic functions, the Gamma function, the elliptical integral, Bessel's functions, and more. With Meijer's G-function, many integrals that could otherwise only be evaluated numerically can instead be expressed in closed form. For this reason, modern computer algebra systems such as Maple contain an implementation of Meijer's G-function. The implementation may be strictly symbolic, or it may also be accompanied by numerical code.
Maple's implementation of Meijer's G-function does come with such a numerical implementation. Unfortunately, this implementation does not always give the right answers.
Recently, I was working on some complicated integrals that Maple was able to evaluate, but only with the help of Meijer's G-function. When I was trying to use these results in a nonlinear least squares estimator, however, I got nonsensical results. I investigated and found that the problem occurred within the MeijerG function. All instances of Meijer's G-function were of the form
\[G^{3,0}_{1,3}\begin{pmatrix}x&\left|\begin{matrix}&a_1&\\b_1&b_2&b_3\end{matrix}\right.\end{pmatrix},\]
with the ai and aj having integral or half-integral values. But when I plot, say, the function
\[G^{3,0}_{1,3}\begin{pmatrix}x&\left|\begin{matrix}&a_1&\\-1/2&-1&-3/2\end{matrix}\right.\end{pmatrix},\]
instead of a nice, smooth analytic curve here is what I get:
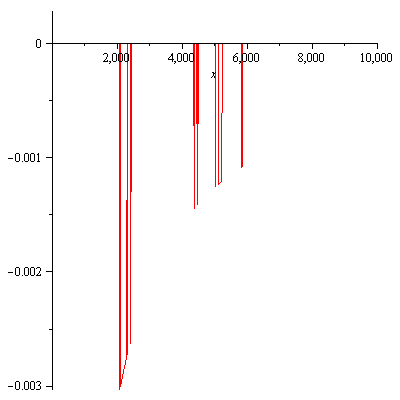
The problem, it turns out, is probably related to the fact that Meijer's G-function exhibits peculiar behavior when any of the differences bi – bj have an integer value. Meijer's G-function can often be calculated using the generalized hypergeometric function, but not in this particular case. Maple is still able to provide numerical results, so it probably uses some alternative formulation when this condition applies. This suggested a solution: what if I perturb these variables a little?
So I wrote a small wrapper function that accomplished just that:
MeijerG3013:=(a1,b1,b2,b3,x)->MeijerG([[],[a1]],[[b1,b2+1e-9,b3-1e-9],[]],x);
Plotting confirms that this replacement behaves smoothly, as we hoped:
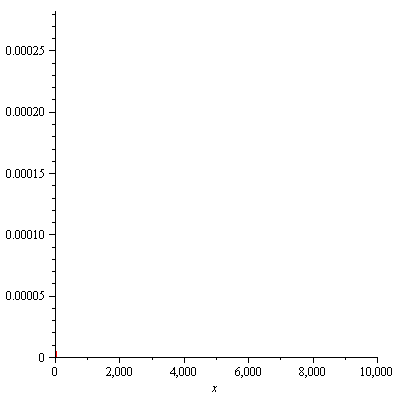
My solution is specific to Meijer's G-function with this particular parameter pattern, but a similar approach may work in other cases, too. Or, it may not. I found that in at least one case, MeijerG3013 continued to behave erratically, but only when called repeatedly from within Maple's LSSolve, no doubt an artifact related to Maple's internal caching functionality. In this particular case, limiting the parameter x to values less than 1000 solved the problem with no appreciable loss of precision in the final result.
Perhaps Maple will fix this issue in an upcoming version. Which I may or may not purchase... I certainly won't, if they continue to use Activation technology to lock licenses to workstations...