This was really driving me nuts. The so-called "barometric formula". Here's what it is all about: an ideal gas in a container of a given volume would fill that volume at constant pressure $p$ and temperature $T$ so that the ideal gas law applies:
\[pV=RnT,\]
where $T$ is the temperature, $n$ is the number of gas molecules (or number of moles, it's just a matter of picking a consistent set of units) and $R$ is the universal gas constant.
So what happens if you put this container in a homogeneous gravitational field characterized by the acceleration constant $g$? Something has to change. Assuming that the temperature of the gas remains constant, the difference in pressure is simply the difference in the weight of a column of gas, which is expressed by the so-called aerostatic equation:
\[dp=-g\rho~dz,\]
where $\rho=\rho(z)$ is the density of the gas at height $z$. The infinitesimal version of the ideal gas law is $p~dV=RT~dn$ but $dn=(dn/dV)dV=(\mu dn/dV)/\mu~dV=\rho/\mu~dV$ where $\mu$ is the particle (or molar) mass, so
\begin{align}p~dV&=\frac{RT}{\mu}\rho~dV,\\\rho&=\frac{\mu p}{RT}.\end{align}
Putting this expression into the aerostatic equation gives
\begin{align}dp&=-\frac{g\mu p}{RT}dz,~~~~{\rm or}\\\frac{1}{p}dp&=-\frac{g\mu}{RT}dz.\end{align}
This last equation can be trivially integrated, producing the barometric formula:
\[p=p_0e^{-g\mu/RT}.\]
This looks nice, but why should we believe that $T$ remains constant with altitude, in this case? Indeed, Feynman himself says, when he introduces the barometric formula, that it really doesn't apply to our atmosphere since the temperature of air varies with altitude. There are at least two intuitive reasons to think that temperature would vary with altitude even in an equilibrium. First, if one imagines a gas as a bunch of little rubber balls that are being shaken, it stands to reason that only the faster balls reach beyond a certain altitude; so while high up, there will be fewer balls, they'd also tend to be "hotter" (keeping in mind that temperature is just the average kinetic energy of a particle.) Another way of looking at it is to think about a house in the summer: it's hot in the attic, cold in the basement, and there really is no reason to believe that, if the house were wrapped with a perfect insulating material, the temperatures would necessarily equalize. Or would they?
So let me rephrase the question. Instead of asking about the change in pressure in an isothermal column of gas, let me ask this: What is the equilibrium state of a column of gas in a homogeneous gravitational field? Equilibrium in this case need not mean isothermal. It may mean isothermal, but that has to be proven. What equilibrium means is that the system is in a state of maximum entropy.
How can we find the equilibrium state? We have two differential equations. One is the ideal gas law, the other is the aerostatic equation, but now both need to be modified to account for the variability of $T$. Two equations are not sufficient to solve for three unknown functions ($T$, $p$ and $\rho$), but we also have a third condition: in the equilibrium state, entropy is maximal.
Using a fundamental equation from thermodynamics,
\[T~dS=dU+p~dV,\]
we can express the infinitesimal change in entropy, $dS$ (here, $dU$ is the infinitesimal potential energy, $dV$ is the volume element, both of which are calculable from $\rho$ and $z$). The condition for equilibrium is that the integral $\int~dS$ be maximal, which is a problem from the calculus of variations. Unfortunately, I was not able to obtain a solution this way. To get to this point, I'd have to be able to express $p$, $\rho$ and $T$ using a function that has appropriate boundary conditions (e.g., $m(z)$ representing the mass of gas in the column up to a height $z$, so that $m(0)=0$ and $m(H)=M$ is the total mass of gas) so that I could have an equation like
\[\int~dS=\int L(m,dm/dz,z)~dz,\]
from which an Euler-Lagrange equation can be obtained and solved for $m$. Well, I couldn't do it, and it is possible that no such nice, clean solution exists.
Fortunately, shortly before I was ready to go bonkers, I came across a paper1 that addressed precisely this problem, i.e., why is $T={\rm const.}$?
Here's the essence of the argument: The particles of the gas would indeed be bouncing about, and only those with more kinetic energy will bounce up high enough to get to the upper reaches of the column. But, by the time they get up there, they'll have lost much of their kinetic energy! So whatever particles get all the way up there will have the same velocity distribution (hence, the same temperature) as the particles at ground level. So, the barometric formula is, in fact, the correct formula, because an equilibrium system will be isothermal.
Unlike my failed attempt, which was to use the axioms of thermodynamics, this reasoning starts with statistical physics. The starting point is the idea that the number of particles located at altitude between $z_1$ and $z_1+dz_1$, and moving at velocities $v_1$ and $v_1+dv_1$ can be expressed using a distribution function $f(z_1,v_1,t_1)$:
\[N=f(z_1,v_1,t_1)~dz_1dv_1.\]
Let us denote the area element $dz_1dv_1$ as $d\tau_1$.
As the system evolves from $t_1$ to $t_2$, the particles move from $z_1$ to $z_2$ and their velocities change from $v_1$ to $v_2$, in accordance with the dynamical equations of the system. However, the particle number remains unchanged, therefore
\[f(z_1,v_1,t_1)d\tau_1=f(z_2,v_2,t_2)d\tau_2.\]
If we could somehow show that $d\tau_1=d\tau_2$, that would mean that the distribution function is independent of time.
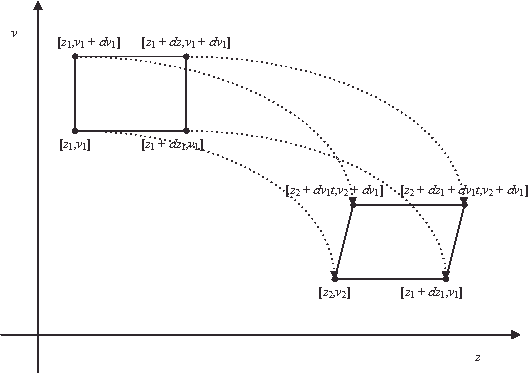
Let us take the special case of the homogeneous gravitational field. Initially, the area element is located in the $[z,v]$ phase space at coordinates $[z_1,v_1]$, $[z_1+dz_1,v_1]$, $[z_1,v_1+dv_1]$, $[z_1+dz_1,v_1+dv_1]$. As the system evolves and $t$ time elapses ($t=t_2-t_1$), the four corners of this rectangle move in accordance with the equations
\begin{align}z_2&=z_1+v_1t+\frac{1}{2}gt^2,\\v_2&=v_1+gt.\end{align}
Therefore, the four corners of the area element are mapped as follows (see also Fig. 1):
\begin{align}[z_1,v_1]&\rightarrow[z_2,v_2],\\ [z_1+dz_1,v_1]&\rightarrow[z_2+dz_1,v_2],\\ [z_1,v_1+dv_1]&\rightarrow[z_2+dv_1t,v_2+dv_1],\\ [z_1+dz_1,v_1+dv_1]&\rightarrow[z_2+dz_1+dv_1t,v_2+dv_1].\end{align}
These corners define a parallelogram with area $dz_1dv_1$, hence
\[d\tau_2=dz_1dv_1=d\tau_1,\]
which means that
\[f(z_1,v_1,t_1)=f(z_2,v_2,t_2).\]
Now let us make an assumption, a very reasonable one on thermodynamical grounds: namely that at some point $t_1$ in time, at some height $z_1$, the distribution function is the Maxwell-distribution:
\[f(z_1,v_1,t_1)=Ce^{-mv_1^2/2RT}.\]
Here, $C$ is a constant, $T$ is the temperature, and $m$ is the mass of a particle.
If the particles move in a collisionless manner, energy for each particle is conserved. The particle energy is a sum of its potential and kinetic energies:
\[E=mgz+\frac{1}{2}mv^2.\]
Energy conservation means that
\[mgz_1+\frac{1}{2}mv_1^2=mgz_2+\frac{1}{2}mgv_2^2.\]
From this,
\[\frac{1}{2}mv_1^2=mgz_2-mgz_1+\frac{1}{2}mgv_2^2.\]
Putting this expression into the Maxwell distribution equation, we get
\[f(z_1,v_1,t_1)=Ce^{mg(z_2-z_1)/RT}e^{-mv_2^2/2RT}.\]
As per the equality established earlier, this also means that
\[f(z_2,v_2,t_2)=Ce^{mg(z_2-z_1)/RT}e^{-mv_2^2/2RT}.\]
The first part of the right-hand side is a function of positions only. The velocity-dependent part of the distribution (hence, the relative probabilities of different velocities) is the same as before. In other words, the temperature is the same, regardless of the altitude; only the density of the medium varies with height.
One obvious question is whether this can be generalized to an arbitrary potential function, not just a homogeneous potential. A key step in the reasoning was the proof that the area element dτ remains unchanged over time. We proved this in the special case of an homogeneous field, but that method doesn't work in the general case.
There is, however, a very powerful theorem in mechanics that is exactly about this issue: Liouville's theorem, that states that a volume element in phase space is a constant of the motion, hence it remains unchanged as we advance time and move along a particle's trajectory. This is exactly what we are saying: $d\tau_1=d\tau_2$.
In the general case, our distribution function will therefore take the form,
\[f(z_2,v_2,t_2)=Ce^{[V(z_2)-V(z_1)]/RT}e^{-mv_2^2/2RT},\]
where $V$ is a potential function. So long as $V$ is a function of only the coordinates, not velocities or time, the result stands: a column of ideal gas in equilibrium will be isothermal.
And, although we only considered the one-dimensional case here, the reasoning can be easily extended to more dimensions, and fields such as the central gravitational field of a planet like the Earth.
So why is the Earth's atmosphere not isothermal, then? Mainly because it is not an equilibrium system! It is constantly heated by the Earth itself from below, it exchanges heat with the oceans, it is heated by the Sun during the day, cooled radiatively during the night... a very complex system indeed, which is why global warming, for instance, remains such a contentious issue.
1Charles A. Coombes and Hans Laue: "A paradox concerning the temperature distribution of a gas in a gravitational field", Am. J. Phys, 53 (3) March 1985