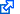As part of my work on the Solar Gravitational Lens, I spent a lot of time thinking about coronagraphs. This led to an interesting insight and a new appreciation of the use of Fourier transforms to describe optical systems.
Coronagraphs are designed to produce a "simulated eclipse", allowing us to see faint objects in the vicinity of something bright, such as the Sun, by blocking light from the bright object.
Unfortunately it is not as simple as it sounds, due to the wave nature of light. Fine spatial details are lost. The Sun or star that we wish to block no longer has a sharp edge. As a result, there'll be some leakage of light around the object that is blocking sunlight.
This is not a problem when the occulter is as big as the Moon! But if you want to block light from the Sun inside the optics of a telescope, it's not so simple.
This problem was solved by the French astronomer Bernard Lyot in the 1930s. Before I explain how, though, first think about how an ordinary projection lens works.
Take a lens. Illuminate it by a point source of light, say, a distant star. Notice that every point on the surface of the lens receives the same amount of illumination. The light front is roughly uniform.
How can such a lens even form an image? The secret lies in the phase of the signal. When the lens focuses light from the point source into the image plane, light rays from different parts of the lens arrive with different phases. In most cases, they will cancel out each other, except for one spot where all the light rays arrive with a coherent phase. That's the spot in the image plane where the image of the point source appears.
You can also intuit that the farther a light ray comes from as measured from the centerline of the lens, the more rapidly its phase can change with that distance from the centerline. This translates into finer spatial detail. Unfortunately, as the diameter of the lens is finite, there is a limit. And when you think about it, this establishes a direct relationship between the spatial frequency of detail in the image plane vs. distance from the centerline of the lens in the lens plane. Which is exactly how a Fourier transform works.
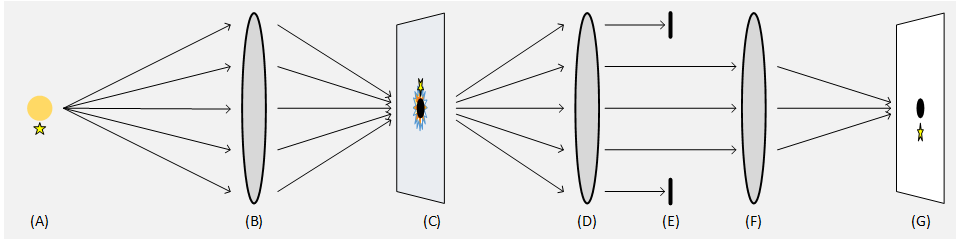
So let's look at the Sun with a nearby star (A) using such a lens (B). As mentioned, the lens represents a Fourier transformed version of the image; as it focuses light into the image plane, the Fourier transform is reversed. In the image plane (C), then, there's an image of the Sun, but it is imperfect. Some spatial detail is lost. This shows up as a circular pattern around the image of the Sun in the image plane. (This is the famous Airy pattern). This is a direct result of the finite spatial resolution due to the finite size of the initial lens. The diameter of that lens effectively works as a low pass filter, removing high frequency details, making the projected image of the Sun blurry. So we can block out the solar disk with a circular occulter but not the blur. There will be a lot of light leakage.
So instead of viewing the image in the image plane, let it pass through. Let it hit another lens (D). Once again, we are in Fourier space. All those high spatial frequency artifacts that made the image of the Sun blurry and could not be removed by the occulter? The are now represented by light rays that travel farthest from the centerline of the lens.
So make the aperture a little smaller! (E) By doing so, yes, we lose a little light and a little spatial resolution, but we also lose all that blur around the (now blocked) solar disk, all that light in the Airy pattern. Finally, we can use a third lens (F) to focus light into the final image plane (G) where we now see the Sun blocked out by the occulter; the blurry Airy pattern blocked out in turn by the narrow aperture (E); so all that remains is a mostly black sky with the star near the Sun, which would have been lost in the Sun's glare, now visible.
So to sum up: we have source (A), Fourier transformed to a lens plane (B), inverse Fourier transformed into an image plane (C) where the solar disk is blocked, Fourier transformed into a second lens plane (D), after which high spatial frequency artifacts are filtered by a narrower aperture (E), and ultimately, yet another lens (F) performs the inverse Fourier transform and we get the desired image (G).
I just love it how the Lyot stop allows us to visualize and understand intuitively how Fourier optics works.