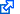This page contains a simulation using the simplest quantitative epidemiological model, the SIR (Susceptible-Infectious-Recovered) model, using current information about the COVID-19 pandemic and comparison to US data. Not exactly physics but... close enough.
But first... why US data? I consider global data unreliable, as it includes data from countries that censor or manipulate information. Furthermore, it includes data from countries that have instituted measures of various efficacy at different times.
US data, in turn, comes from a large country so it represents a statistically significant sample, it is fairly reliable, and it comes from a country that, unfortunately, has been less than effective so far in its attempt to contain the outbreak. As a result, the SIR model matches American reality alarmingly well so far.
The SIR model has three variables and two parameters. The three variables are all numbers between 0 and 1, representing the ratio of the population who are susceptible $(S),$ infected $(I),$ or recovered $(R).$ The two parameters, customarily denoted by $\beta$ and $\gamma,$ can be thought of as representing the inverse of the typical time between contacts by an infected person and the inverse of the typical time to recovery. Their ratio, $R_0=\beta/\gamma,$ is the famous Basic Reproduction Number. For COVID-19, without preventative measures such as social distancing, $R_0\sim 2.35$ according to the literature that I have seen.
The system of equations that constitute the SIR model is a system of three first-order differential equations that can be integrated numerically with ease:
$$\begin{align*}
\frac{dS}{dt}&=-\beta IS,\\
\frac{dI}{dt}&=\beta IS-\gamma I,\\
\frac{dR}{dt}&=\gamma I.
\end{align*}$$
The charts below show the predictions of the SIR model for the next several months using present-day US data as initial conditions, and a comparison with US data from early March (when the US infection rate first hit one person in a million) up to now. The data set is current as of .
Feel free to play with the numbers below. The lower the value $\Sigma^2$, the better the agreement between model and data. Of course if you enter crazy values, expect crazy results.
Initially (late March) the data matched the SIR model predictions quite well (and the results were alarming.) Later (early April) the data deviated from the model downward, which was a hopeful sign: a possible indication that mitigation measures are working and that the curve is being "flattened" by lockdowns and social distancing.
Unfortunately, as the days went by, reality began to deviate from the model's optimistic predictions. With each and every passing day, there are more cases than the model predicts. The expected decline has not materialized yet, and by late April, the model began to perform increasingly poorly. By June, for reasons that are political, not epidemiological, US numbers were out of control. Yet it seems that the law of averages/large numbers applies: by mid-October, despite the ups and downs, the model shows a surprisingly decent fit, though of course predicting a much higher toll now than it did months ago. For what it's worth, in many other countries, Canada included, reality follows a similar route: the numbers are lower but there are new waves of infections and the end is not yet in sight.
Model parameters
| $I_0$: | Initial number of patients on March 6, 2020 | |
| $\beta$: | Inverse of typical time between contacts | |
| $\gamma$: | Inverse of typical recovery time | |
| $R_0$: | Basic Reproduction Number | |
| $\Sigma^2$: | Sum of squared difference between US data and SIR model |
SIR model prediction for the United States