I have been troubled by this for a long time. Gravitational collapse is described by variations of a solution first obtained by Oppenheimer and Snyder in 1939. A collapsing sphere of dust, to outside observers, has the static gravitational field of a point mass, i.e., the Schwarzschild solution. The interior of the dust sphere is homogeneous, and the field equations describing it are those of a collapsing spacetime, i.e., the Friedmann–Lemaître–Robertson–Walker solution.
But what about the boundary? Most importantly, is there still a boundary beyond the event horizon, as depicted (but usually not well elaborated on) in many textbooks? Or is it possible that inside the event horizon, we have a homogeneous collapsing dust cosmology, no boundary and no vacuum region?
I strongly suspected the latter and spent many months trying to think of a way to find robust proof. My logic was simple: The event horizon is determined by the last moments in time when a particle inside the dust cloud can still send a signal to the surface, with the signal reaching the surface before the collapse is complete, i.e., before the final singularity.
My logic was also flawed.
But it was only the other day that I was finally able to ask the right question, the answer to which exposed the flaw in my thinking.
There really are two distinct questions to ask. Let us consider, for simplicity, the particle at the center of the dust cloud:
- What is the last moment in time when this particle can send a signal that reaches the dust cloud surface before collapse is complete?
- What is the last moment in time when this particle can send a signal that escapes the dust cloud and reaches future infinity?
Unless the two values coincide, there will be a period of time when the particle inside the dust cloud can send a signal to the dust cloud surface, but the signal cannot escape to infinity anymore: i.e., when it reaches the surface, it's beyond the horizon, and the vacuum region the signal enters is also beyond the event horizon. Thus, a vacuum region necessarily exists beyond the horizon.
So let us calculate, then. We start with the standard FLRW metric with positive spatial curvature, which can be written in the form
\begin{align}
ds^{2}=-d\tau^{2}+a(\tau)^{2}\Big(d\chi^{2}+\sin^{2}\chi\,d\Omega^{2}\Big).\tag{1}
\end{align}
We then introduce conformal time $\eta$ via $d\tau=a(\eta)\,d\eta$, so that
\begin{align}
a(\eta)&{}=\frac{a_0}{2}\big(1+\cos\eta\big),\\
\tau(\eta)&{}=\frac{a_0}{2}\big(\eta+\sin\eta\big),\tag{2}
\end{align}
Maximum expansion $(a(\eta)=a_0)$ happens at $\eta=0$, whereas the singularity occurs at $\eta=\pi$. The surface radius in coordinates that are compatible with the exterior Schwarzschild spacetime is given by
\begin{align}
r_b(\eta)=a(\eta)\sin\chi_0,\tag{3}
\end{align}
where $\chi_0$ is the (constant) radius of the dust sphere in comoving coordinates.
In conformal coordinates, radial null geodesics are characterized by
\begin{align}
\frac{d\chi}{d\eta}=\pm 1.\tag{4}
\end{align}
Answering our first question is now trivially easy: the last signal that the particle at the center can send that would reach the surface of the dust sphere before the singularity must be emitted at conformal time
\begin{align}
\eta_{e,\max}=\pi-\chi_0.\tag{5}
\end{align}
So then, what would be the conformal time of emission of a signal that reaches the dust surface before it forms a horizon? The latest such signal would reach the surface when $r_b(\eta_{b,\infty})=2M$ where $M$ is the Schwarzschild (ADM) mass of the collapsing sphere. Let us do the math. Given $r_0=a_0\sin\chi_0$, we have
\begin{align}
r_b(\eta_{b,\infty})&{}=\frac{r_0}{2}(1+\cos\eta_{b,\infty}),\\
\frac{4M}{r_0}-1&{}=\cos\eta_{b,\infty}.\tag{6}
\end{align}
In the Oppenheimer–Snyder solution, we have the matching relation $\sin^2\chi_0=2M/r_0$. Therefore:
\begin{align}
2\sin^2\chi_0-1&{}=\cos\eta_{b,\infty},\\
-\cos 2\chi_0&{}=\cos\eta_{b,\infty},\\
\eta_{b,\infty}&{}=\pi-2\chi_0.\tag{7}
\end{align}
The corresponding conformal time of emission, then, is
\begin{align}
\eta_{e,\infty}&{}=\pi-3\chi_0.\tag{8}
\end{align}
Thus we reach the inevitable consequence that a signal emitted by the central particle of the Oppenheimer–Snyder dust cloud at conformal time
\begin{align}
\pi-3\chi_0<\eta<\pi-\chi_0\tag{9}
\end{align}
will reach the dust surface and exit the cloud but cannot escape to infinity. This proves that a vacuum region must exist inside the event horizon.
This result can also be depicted graphically in the form of a conformal diagram:
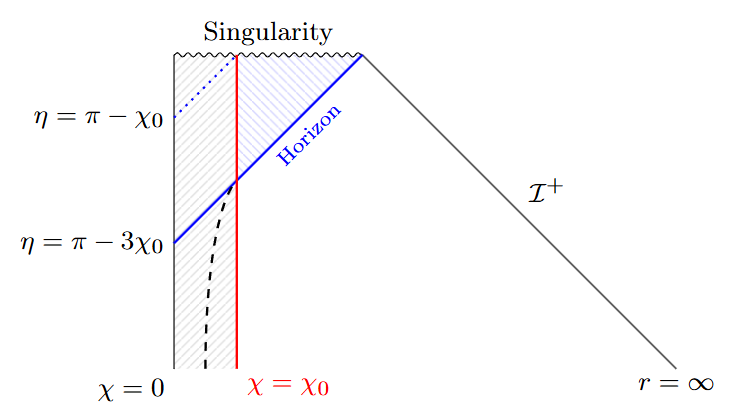
The event horizon of course corresponds to the last moment in time (conformal time $\eta=\pi-3\chi_0$) when a signal can be emitted and escape to infinity. A dotted line shows the last signal that can be emitted (at $\eta=\pi-\chi_0$) to reach the dust surface before the singularity. The blue shaded region is the vacuum region inside the horizon. The curvy dashed line starting from the bottom corresponds approximately to the $r=2M$ Schwarzschild radius: it eventually smoothly merges into the $r=2M$ null surface of the horizon in the exterior Schwarzschild spacetime.
This diagram also explains why the horizon is sometimes described as "teleological". At the center of the dust sphere, the horizon begins at conformal time $\eta=\pi-3\chi_0$. However, nothing special takes place at this time at this location. The existence of the horizon here depends on the future behavior of the dust. If the dust sphere explodes before completing collapse (at conformal time $\pi-2\chi_0$) no horizon may form at all. Yet the spacetime geometry at $\chi_0, \eta=\pi-3\chi_0$ remains unaffected by this future event.
Thus I learned that for months, I was laboring under an appealing but ultimately false assumption*. No, the interior of the event horizon formed by Oppenheimer–Snyder collapse is not a homogeneous FLRW mini-universe. It is a homogeneous collapsing dust cloud characterized by the FLRW metric, surrounded by vacuum that is characterized by a standard interior Schwarzschild vacuum solution, which can be described if necessary, e.g., using Eddington–Finkelstein or Kruskal–Szekeres coordinates.
*Thanks in particular to Andrew Hamilton who patiently helped, pointing my nose in the right direction.