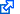Thermal engineers often use so called dry bulb and wet bulb temperatures as a measure of humidity in the air. Dry bulb temperature reflects what a dry thermometer measures. A wet thermometer measures a lower temperature due to evaporative cooling, unless the relative humidity is 100%.
The conversion between wet-bulb and dry-bulb temperatures is surprisingly non-trivial. Full details can be found in Chapter 6 of the ASHRAE Fundamentals handbook. (My notation differs slightly from ASHRAE's.)
To convert between the two, you need to know either the dry-bulb or the wet-bulb temperature, in addition to atmospheric pressure and relative humidity. In metric units, the calculation goes as follows. First, absolute temperature ($T$, in Kelvin) is related to the Celsius scale ($t$) as
$$T=t+273.15.$$
You can compute the saturation water pressure for a given absolute temperature:
$$\ln p_{\rm ws}(T)=\sum_{i=-1}^4C_iT^i + C_l\ln T,$$
where the coefficients have different values for $t<0~^\circ{\rm C}$ and $t>0~^\circ{\rm C}$ (i.e., below and above freezing). For the former,
\begin{align}
C_{-1}&=-5.800 220 6\times 10^3,\\
C_0&=1.391 499 3,\\
C_1&=-4.864 023 9\times 10^{-2},\\
C_2&=4.176 476 8\times 10^{-5},\\
C_3&=-1.445 209 3\times 10^{-8},\\
C_4&=0,\\
C_l&=6.545 967 3,
\end{align}
whereas for the latter (above freezing),
\begin{align}
C_{-1}&=-5.674 535 9\times 10^{-3},\\
C_0&=6.392 524 7,\\
C_1&=-9.677 843 0\times 10^{-3},\\
C_2&=6.221 570 1\times 10^{-7},\\
C_3&=2.074 782 5\times 10^{-9},\\
C_4&=-9.484 024 0\times 10^{-13},\\
C_l&=4.163 501 9.
\end{align}
From $p_{\rm ws}$ and the pressure $p$, the humidity ratio at saturation can be calculated:
$$W_s(T,p)=0.62198\frac{p_{\rm ws}(T)}{p-p_{\rm ws}(T)}.$$
Given a relative humidity $\phi$ at dry-bulb temperature $T_{\rm db}$, the water vapor pressure is given by
$$p_w(T_{\rm db},\phi)=\phi p_{\rm ws}(T_{\rm db}),$$
and if the pressure and water vapor pressure are known, the humidity ratio can be calculated as
$$W(T_{\rm db},p,\phi)=0.62198\frac{p_w(T_{\rm db},\phi)}{p-p_w(T_{\rm db},\phi)}.$$
Finally, the relationship between dry-bulb and wet-bulb temperature is given implicitly by the following equations. First, above freezing:
$$W(T_{\rm db},p,\phi)=\frac{(2501-2.326t_{\rm wb})W_s(T_{\rm wb},p)-1.006(t_{\rm db}-t_{\rm wb})}{2501+1.86t_{\rm db}-4.186t_{\rm wb}},$$
and below freezing:
$$W(T_{\rm db},p,\phi)=\frac{(2830-0.24t_{\rm wb})W_s(T_{\rm wb},p)-1.006(t_{\rm db}-t_{\rm wb})}{2830+1.86t_{\rm db}-2.1t_{\rm wb}}.$$
These equations can be solved numerically to obtain the desired temperature from the other value. There is no closed form solution.