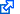Here is a neat problem that I spent a lot of time trying to solve when I was around ten. Around forty years ago.
I already learned about simple electronic circuits. In particular, I learned the rules to calculate resistance when resistors are connected in series:

$$R=R_1+R_2.$$
or, when they are connected in parallel:
$$R=\frac{1}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}}.$$
But... what about a resistor bridge?
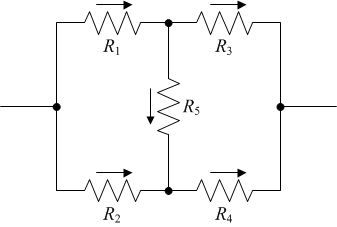
For the life of me, I could not figure it out. No matter what clever combination I tried, I could not reduce this circuit to a combination of series- and parallel-connected resistors.
Today, of course, I know better: it just cannot be done. What needs to be done, instead, is an application of Kirchoff's laws for circuits. Kirchoff's current law is that the sum of currents entering and exiting a node (junction) will always be zero. Kirchoff's voltage law is that the sum of voltages over any closed circuit will be zero.
So then, remembering that $U=RI$, here are five equations for the five currents flowing through the five resistors:
\begin{align*}
R_1I_1-R_2I_2+R_5I_5&=0,\\
R_3I_3-R_4I_4-R_5I_5&=0,\\
R_1I_1-R_2I_2+R_3I_3-R_4I_4&=0,\\
I_1-I_3-I_5&=0,\\
I_2-I_4+I_5&=0.
\end{align*}
Unfortunately this set of equations is not independent. We need one more equation to make the system solvable. For instance, we may assume that we know the total voltage $U$ applied to the circuit, which yields:
$$R_1I_1+R_3I_3=U.$$
Ultimately, what we are interested in is $I_1+I_2$ as, in combination with $U$, it will yield the resistance of this circuit:
$$R=\frac{U}{I_1+I_2}.$$
So then, let's do a little algebra. First, eliminate $I_3=(U-R_1I_1)/R_3$:
\begin{align*}
R_1I_1-R_2I_2+R_5I_5&=0,\\
R_1I_1+R_4I_4+R_5I_5&=U,\\
(R_1+R_3)I_1-R_3I_5&=U,\\
I_2-I_4+I_5&=0.
\end{align*}
Next, use the last equation to eliminate $I_2=I_4-I_5$:
\begin{align*}
R_1I_1-R_2I_4+(R_2+R_5)I_5&=0,\\
R_1I_1+R_4I_4+R_5I_5&=U,\\
(R_1+R_3)I_1-R_3I_5&=U.
\end{align*}
Using the last equation we can eliminate $I_5=[(R_1+R_3)I_1-U]/R_3$:
\begin{align*}
[R_1R_3+(R_2+R_5)(R_1+R_3)]I_1-R_2R_3I_4&=(R_2+R_5)U,\\
[R_1R_3+(R_1+R_3)R_5]I_1+R_3R_4I_4&=(R_3+R_5)U.
\end{align*}
Multiplying the first of these equations by $R_4$, the second by by $R_2$, and adding them eliminates $I_4$:
\begin{align*}
I_1&=\frac{(R_2+R_5)R_4+(R_3+R_5)R_2}{R_1R_3(R_2+R_4)+(R_1+R_3)(R_2+R_5)R_4+(R_1+R_3)R_2R_5}U.
\end{align*}
Now,
\begin{align*}
I_2=\frac{R_1I_1+R_5I_5}{R_2}=\frac{R_1I_1+R_5[(R_1+R_3)I_1-U]/R_3}{R_2}=\frac{[R_1R_3+(R_1+R_3)R_5]I_1-R_5U}{R_2R_3},
\end{align*}
thus
\begin{align*}
I_1+I_2&=\frac{[(R_1+R_2)R_3+(R_1+R_3)R_5]I_1-R_5U}{R_2R_3}\\
&=\frac{\dfrac{[(R_1+R_2)R_3+(R_1+R_3)R_5][(R_2+R_5)R_4+(R_3+R_5)R_2]}{R_1R_3(R_2+R_4)+(R_1+R_3)(R_2+R_5)R_4+(R_1+R_3)R_2R_5}-R_5}{R_2R_3}U\\
&=\frac{\dfrac{[(R_1+R_2)R_3+(R_1+R_3)R_5][(R_3+R_4)R_2+(R_2+R_4)R_5]}{R_1R_3(R_2+R_4)+(R_1+R_3)(R_2+R_4)R_5+R_2R_4(R_1+R_3)}-R_5}{R_2R_3}U\\
&=\frac{(R_1+R_2+R_3+R_4)R_5+(R_1+R_2)(R_3+R_4)}{(R_1+R_3)(R_2+R_4)R_5+(R_1+R_2)R_3R_4+R_1R_2(R_3+R_4)}U,
\end{align*}
where the final form demonstrates the symmetry of the result. Therefore,
$$R=\frac{U}{I_1+I_2}=\frac{(R_1+R_3)(R_2+R_4)R_5+(R_1+R_2)R_3R_4+R_1R_2(R_3+R_4)}{(R_1+R_2+R_3+R_4)R_5+(R_1+R_2)(R_3+R_4)}.$$
What a beautiful result! There was a time (again, back forty years ago) when I actually believed that with series resistors, parallel resistors, and the resistor bridge, all circuits are solvable. Alas, that is not the case: there are circuits one can construct that cannot be broken down into combinations of these three elementary circuits. In any case, the formulae get progressively complicated, so rather than working them out in the general case, it is easier to just use Kirchoff's laws and solve each circuit individually. Of course nowadays, with circuit analysis software readily available, this is not something people need to do by hand very often...